本文共 2454 字，大约阅读时间需要 8 分钟。

1. DNS是什么

DNS（DomainName System）域名系统，在TCP/IP网络中有非常重要的地位，能够提供域名与IP地址的解析服务。

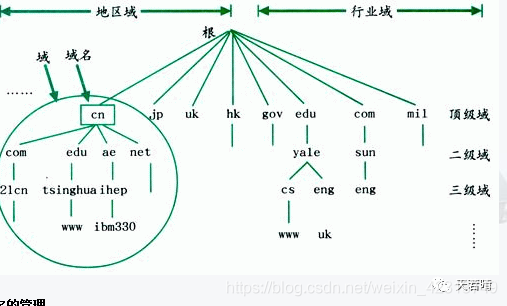
DNS是一个分布式数据库，命名系统采用层次的逻辑结构，如同一棵倒置的树，这个逻辑的树形结构称为域名空间，由于DNS划分了域名空间，所以各机构可以使用自己的域名空间创建DNS信息。

注：DNS域名空间中，树的最大深度不得超过127层，树中每个节点最长可以存储63个字符。

2. 域和域名

• 域：DNS树的每个节点代表一个域，通过这些节点，对整个域名空间进行划分，成为一个层次结构。域名空间的每个域的名字，通过域名进行表示。
• 域名：通常由一个完全合格域名（FQDN）标识。FQDN能准确表示出其相对于DNS域树根的位置，也就是节点到DNS树根的完整表述方式，从节点到树根采用反向书写，并将每个节点用“.”分隔，对于DNS域google来说，其完全正式域名（FQDN）为google.com。

说明：FQDN：(FullyQualified Domain Name)全限定域名：同时带有主机名和域名的名称。（通过符号“.”）

例如：google为com域的子域，其表示方法为google.com，而www为google域中的子域，可以使用www.google.com表示。 注意：通常，FQDN有严格的命名限制，长度不能超过256字节，只允许使用字符a-z,0-9,A-Z，域名不区分大小写。

以www.baidu.com为例

根域名是com、顶级域名是baidu.com、主域名是www.baidu.com

由最顶层到下层，可以分成：根域、顶级域、二级域、子域。

3. 主域名服务器与辅助域名服务器的关系

• 当区的辅助服务器启动时，它与该区的主控服务器进行连接并启动一次区传输，区辅助服务器定期与区主控服务器通信，查看区数据是否改变。如果改变了，它就启动一次数据更新传输。
• 每个区必须有主服务器，另外每个区至少要有一台辅助服务器，否则如果该区的主服务器崩溃了，就无法解析该区的名称。

辅助服务器的优点：

(1) 容错能力 配置辅助服务器后，在该区主服务器崩溃的情况下，客户机仍能解析该区的名称。一般把区的主服务器和区的辅助服务器安装在不同子网上，这样如果到一个子网的连接中断，DNS客户机还能直接查询另一个子网上的名称服务器。

(2) 减少广域链路的通信量

如果某个区在远程有大量客户机，用户就可以在远程添加该区的辅助服务器，并把远程的客户机 配置成先查询这些服务器，这样就能防止远程客户机通过慢速链路通信来进行DNS查询。

(3) 减轻主服务器的负载

辅助服务器能回答该区的查询，从而减少该区主服务器必须回答的查询数。

4. DNS服务器与缓存

(1) DNS服务器

• 运行DNS服务器程序的计算机，储存DNS数据库信息。DNS服务器会尝试解析客户机的查询请求。
• 在解答查询时，如果DNS服务器能提供所请求的信息，就直接回应解析结果，如果该DNS服务器没有相应的域名信息，则为客户机提供另一个能帮助解析查询的服务器地址。
• 如果以上两种方法均失败，则回应客户机没有所请求的信息或请求的信息不存在。

(2) DNS缓存

• DNS服务器在解析客户机请求时，如果本地没有该DNS信息，则可以会询问其他DNS服务器，当其他域名服务器返回查询结果时，该DNS服务器会将结果记录在本地的缓存中，成为DNS缓存。
• 当下一次客户机提交相同请求时，DNS服务器能够直接使用缓存中的DNS信息进行解析。

5. DNS工作原理

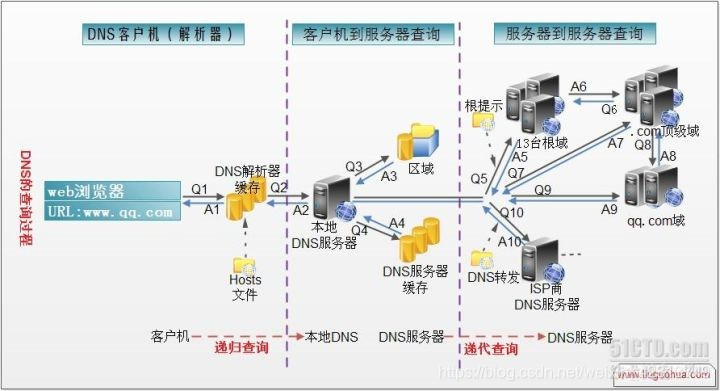
• DNS 查询以各种不同的方式进行解析。客户机有时也可通过使用从以前查询获得的缓存信息就地应答查询。DNS 服务器可使用其自身的资源记录信息缓存来应答查询，也可代表请求客户机来查询或联系其他 DNS 服务器，以完全解析该名称，并随后将应答返回至客户机。这个过程称为递归查询。
• 另外，客户机自己也可尝试联系其他的 DNS 服务器来解析名称。如果客户机这么做，它会使用基于服务器应答的独立和附加的查询，该过程称作迭代，即DNS服务器之间的交互查询就是迭代查询。
• DNS有两种查询方式：递归查询和迭代查询
  

6. 正向解析和反向解析

正向解析：正向解析是指域名到IP地址的解析过程。

反向解析：反向解析是从IP地址到域名的解析过程。反向解析的作用为服务器的身份验证。 例：http://dns.aizhan.com/

7. DNS资源记录类别

1）SOA资源记录

每个区在区的开始处都包含了一个起始授权记录（Startof Authority Record）,简称SOA记录。

SOA定义了域的全局参数，进行整个域的管理设置。一个区域文件只允许存在唯一的SOA记录。

2）NS资源记录

NS（NameServer）记录是域名服务器记录，用来指定该域名由哪个DNS服务器来进行解析。每个区在区根处至少包含一个NS记录。

3）A资源记录

地址（A）资源记录把FQDN映射到IP地址。因为有此记录，所以DNS服务器能解析FQDN域名对应的IP地址。

4）PTR资源记录

相对于A资源记录，指针（PTR）记录把IP地址映射到FQDN。用于反向查询，通过IP地址，找到域名。

5）CNAME资源记录

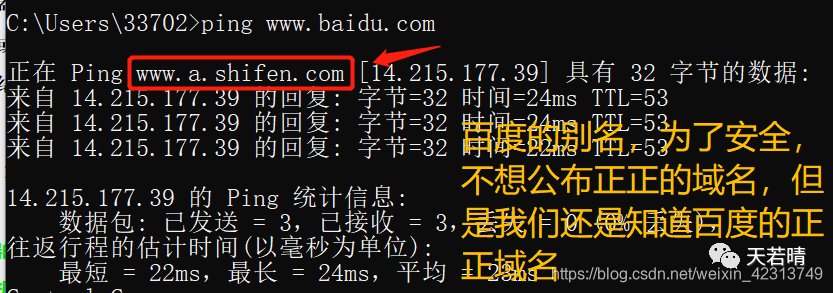
别名记录（CNAME）资源记录创建特定FQDN的别名。用户可以使用CNAME记录来隐藏用户网络的实现细节，使连接的客户机无法知道真正的域名。

例：ping百度时，解析到了百度的别名服务器。百度有个cname=www.a.shifen.com.的别名

6）MX资源记录

邮件交换（MX）资源记录，为DNS域名指定邮件交换服务器。

邮件交换服务器是为DNS域名处理或转发邮件的主机。处理邮件指把邮件投递到目的地或转交另一不同类型的邮件传送者。转发邮件指把邮件发送到最终目的服务器，用简单邮件传输协议SMTP把邮件发送给离最终目的地最近的邮件交换服务器，或使邮件经过一定时间的排队。

转载地址：http://yramz.baihongyu.com/